Semestralni prace z predmetu "Signaly a soustavy"
Zadani
Soubor Sound.wav obsahuje 8-mi bitové vzorky audiosignálu, jenž je zpracováván obvodem na úpravu zvuku, jehož impulsová odezva je v souboru filtr.dat.
- Zobrazte vstupní a výstupní signál a jejich spektra.
- Určete energii vstupního a výstupního signálu.
- Z tvaru a průběhu vstupního, výstupního signálu a impulsové odezvy filtru (případně z jejich spekter) usudte na typ zvukové úpravy.
Prilohy
2_P010-3.pdf - originalni verze zadani
Reseni
Nejdrive provedeme inicializaci prostedi v Matlabu.
clc; clear all; close all; format long;
Vstupni a vystupni signaly
Nacteme vstupni signal a zobrazime ho.
[i,fs,b] = wavread('Sound.wav');
N = length(i);
figure; stem((0:length(i)-1)/fs,i,'.');
title('Vstupni signal');
xlabel('t[s]');
ylabel('s(t)');
grid on;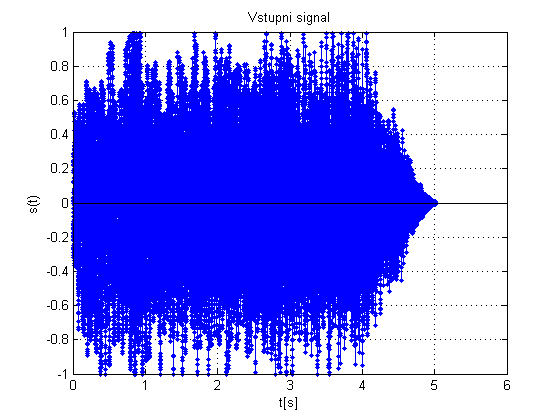
Dale nacteme impulzovou odezvu filtru a zobrazime ji.
f = dlmread('filtr.dat', '\n');
figure; stem((0:length(f)-1)/fs,f);
title('Impulzova odezva filtru');
xlabel('t[s]');
ylabel('s(t)');
grid on;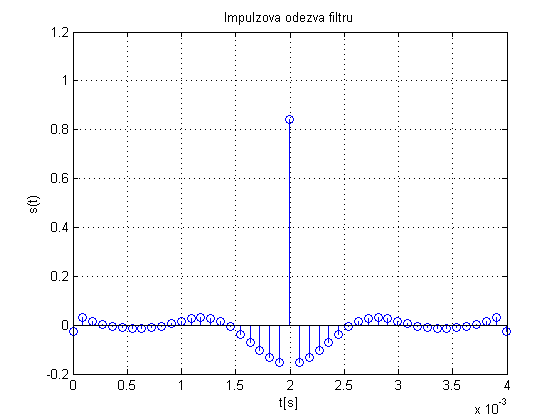
Dalsim krokem je aplikace impulzove odezvy filtru na vstupni signal. To provedeme pomoci konvoluce. Vystup opet zobrazime.
o = conv(i, f);
wavwrite(o, fs, b, 'vystup.wav');
figure; stem((0:length(o)-1)/fs,o,'.');
title('Vystupni signal');
xlabel('t[s]');
ylabel('s(t)');
grid on;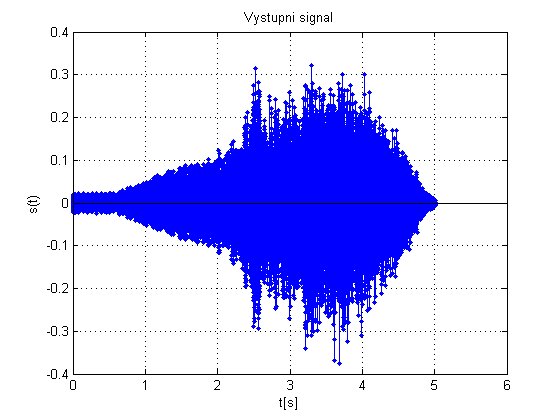
Spektra vstupniho a vystupniho signalu
Spektrum vstupniho signalu ziskame fourierovou transformaci. Uveden je obecny vztah, ale pro konkretni vypocet byla pouzita rychla fourierova transformace (samozrejme diskretni).
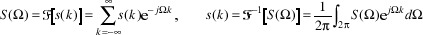
is = fftshift(fft(i));
figure; stem((-length(is)/2:length(is)/2-1)*fs/length(i),abs(is),'.');
title('Spektrum vstupniho sugnalu');
xlabel('f[Hz]');
ylabel('S(f)');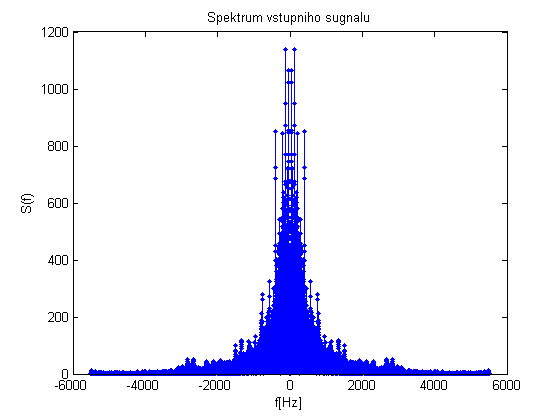
Obdobne i pro vystupni signal.
os = fftshift(fft(o));
figure; stem((-length(os)/2:length(os)/2-1)*fs/length(o),abs(os),'.');
title('Spektrum vystupniho signalu');
xlabel('f[Hz]');
ylabel('S(f)');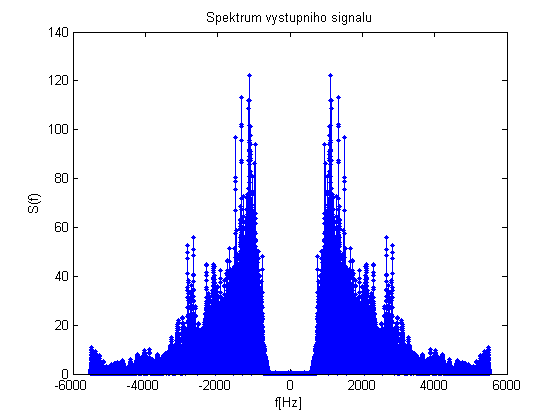
Energie signalu
Nakonec spocitame pozadove hodnoty energii pro vstupni a vystupni signal.
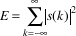
Ein = sumsqr(i) Eout = sumsqr(o) Ein = 5.643853576660156e+003 Eout = 1.793025481292911e+002
Zaver
Je videt, ze se jedna o horni propust.